Alapvetően 26 olyan módszer létezik, melyek mögött átfogó vizsgálatok, bizonyítékok állnak, és melyekről elmondható az, hogy érdemes használni a részvénypiac jövőbeni alakulásának előrejelzésében. Ezek a mutatók, összefüggések a részvénypiac kockázati prémiumát jelzik előre, és mivel a részvények 95 százalékának pozitív a bétája, azaz a tőzsdeindexszel bizonyos fokig együtt mozog a részvények többsége, így egyedi részvényekbe befektetők, passzív befektetők és befektetők széles körének fontos tudni azt, hogy hogyan alakulhat a részvénypiacon a jövőbeni hozam. A témával kapcsolatban egy új vizsgálat 26 összefüggés előrejelzési pontosságát vizsgálta 1891-2020 közötti időszakon. Ennek részleteit beszéljük meg. Témáink:
- Miért fontos a részvénypiac kockázati prémiuma?
- Egyedi részvények esetében is lényeges a kockázati prémium
- Hogyan határozható meg a részvénypiac kockázati prémiuma?
- Melyek a legjobb modellek?
- A jövőbeni hozam három tényezője
- A 26 módszer pontossága 10 éves időtávon
- A 26 módszer pontossága 20 éves időtávon
- Portfólióallokáció a TRCAPE alapján
Miért fontos a részvénypiac kockázati prémiuma?
A részvénypiac kockázati prémiuma azt a többlethozamot jelöli, mellyel a részvények felülteljesítik a kötvényeket. Ahogy az alábbi képen is látható, végtelen időtávon a részvénypiaci kockázati prémiuma pozitív (lásd 1900-2010 közötti átlagokat).
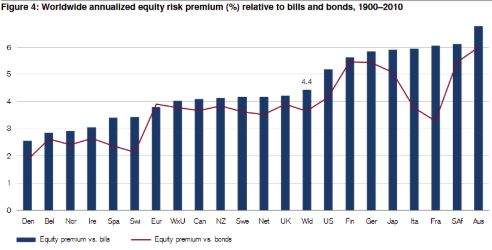
Ugyanakkor rövidebb, az átlagos befektető számára szóba jöhető időtávokon (10-30 év) a részvénypiac kockázati prémiuma volatilis, és múltbeli példák mutatják, hogy akár negatív is lehet, lásd alábbi eseteket a részvénypiac kockázati prémiumára:
- Egyesült Királyság 1980-2000 között: -1,1%
- Belgium 1920-1939 között: -0,5%
- Belgium 1930-1949 között: -0,5%
- Dánia 1920-1949 között: -1,9%
- Franciaország 1960-1979 között: -1,8%
- Németország 1960-1979 között: -1,8%
- Írország 1900-1939 között: -0,6%
- Olaszország 1960-1979 között: -4%
- Hollandia 1910-1939 között: -0,9%
- Spanyolország 1930-1959 között: -0,6%
- Svédország 1910-1949 között: -0,3%
- Svájc 1910-1949 között: -0,5%
A fentiek miatt számos módszert, összefüggést felfedeztek mára, melyek statisztikailag szignifikáns (99 százalékos valószínűséggel nem a véletlen műve) vizsgálatokon alapulnak. Ugyanakkor látni kell azt is, hogy a fentiektől függetlenül is el lehet követni tesztelési hibákat, így a jövőbeni alkalmazhatóság szempontjából az out of sample tesztelések a legértékesebbek. Ennek lényege, hogy az összefüggés felfedezését követően olyan adatokon teszteljük vissza az összefüggést, melyet nem használtak fel a módszer felfedezése során. Ez adja az értékét a néhány hete, a témában megjelent vizsgálatnak, mely összegyűjtött 26 módszert a részvénypiac kockázati prémiumának előrejelzésével kapcsolatban.
Egyedi részvények esetében is lényeges a kockázati prémium
Ahogy a bevezetőben is utaltam rá, a részvénypiac kockázati prémiuma releváns azon befektetők számára is, akik egyedi részvényekben, fókuszált portfólióban gondolkodnak. Ennek oka, hogy az egyedi részvények szoros korrelációt mutatnak a teljes részvénypiaccal. Ehhez a magyarázatot a CAPM modell bétájában találjuk meg, vagy ahogy ez az alábbi, FF5 modell képletében is látható.
Ahogy a bevezetőben is utaltam rá, a részvénypiac kockázati prémiuma releváns azon befektetők számára is, akik egyedi részvényekben, fókuszált portfólióban gondolkodnak. Ennek oka, hogy az egyedi részvények szoros korrelációt mutatnak a teljes részvénypiaccal. Ehhez a magyarázatot a CAPM modell bétájában találjuk meg, vagy ahogy ez az alábbi, FF5 modell képletében is látható.
ERi=Rf+βi(ERm−Rf)+SMB+HML+RMW+CMA
Jelölések:
- ERi: a befektetés/részvény várható hozama
- Rf: kockázatmentes kamat
- βi: a portfólió, részvény bétája
- (ERm-Rf): a részvénypiac kockázati prémiuma, azaz részvénypiac hozama – kockázatmentes hozam.
- SMB, size prémium, lásd itt
- HML, value prémium, lásd itt
- RMW, jövedelmezőségi prémium, lásd itt
- CMA, tulajdonképpen az asset growth hatás
Egyedi részvények hozama tehát több más tényező mellett legfőképpen a részvénypiac kockázati prémiuma és a béta szorzata alapján határozható meg. Ha pedig egy tetszőleges árfolyamszűrőben (lásd finviz.com) megnézzük a részvények béta tényezőit, akkor az esetek 95 százalékában pozitív bétát látunk.
Hogyan határozható meg a részvénypiac kockázati prémiuma?
A fentiekből látható, hogy a részvénypiac kockázati prémiuma 10-20 éves időtávon is jelentősen ingadozhat, és léteznek összefüggések, melyekkel bizonyos fokig meghatározható a prémium jövőbeni alakulása. Ezeknek az alapja részben a gordon-féle modell, melynek képlete a következő.

ahol:
- P0 a piaci ár a mai napon
- D1 a következő évi osztalék
- g az osztalék növekedési üteme
- E(R) a részvénypiac kockázati prémiuma
A fenti egyenletet átrendezve megkapjuk a részvénypiac kockázati prémiumát meghatározó tényezőket, lásd itt:

Azaz a részvénypiac kockázati prémium az osztalékhozam (osztalék és az ár hányadosa) és az osztaléknövekedés üteme alapján határozható meg. A fenti képlet hosszú távon (amit 100 évben definiálunk) stabil eredményt ad a részvénypiac kockázati prémiumára, de rövid távon (ami 10-20 év) ingadozik a prémium.
Ennek két oka van. Az egyik a kockázatalapú megközelítés, azaz a befektetők kockázatvállalási hajlandósága időről időre változik. Ez eredményezi a prémium ingadozását, mert egyes befektetők csak magasabb várható hozam mellett lépnek piacra. A másik okot a viselkedési közgazdaságtan képviselői határozták meg (Robert Shiller professzor). Eszerint egyes időszakokban a részvénypiac túlárazott lesz, amit alacsonyabb kockázati prémium követ, más időszakokban pedig a piac alulárazott, ami magasabb kockázati prémiumot eredményez. Véges időtávon tehát az alábbiak szerint alakul a képletünk:

A ΔV tehát az értékeltség tényezőjét szemlélteti. A fentiek adják az alapját az összes jövőbeni hozamot előrejelző mutatónak bár a fenti három komponenst eltérően mérik.
A jövőbeni hozam három tényezője
Az alábbiakban részletezett tanulmány 26 összefüggést vizsgált meg, melyek előrejelzési módszere alapvetően három pilléren alapul: hozam, hozam és növekedés, értékeltség. Egyes módszerek csak a hozam alapján, mások hozam és növekedés, illetve értékeltség alapján adnak előrejelzéseket. A fent hivatkozott vizsgálatban 1872-2020 közötti időszakon vizsgáltak meg különböző módszerek 10-20 éves időtávra vonatkozó előrejelző képességét. A 26 módszer pontos leírását megtaláljuk a tanulmány 33-34. oldalán. Néhány ismertebbet kiemelnék közülük:
[1] Historical Mean: A tőzsdeindex történelmi átlagát vetítjük ki a jövőben és ez az alapja a hozam-előrejelzésnek.
[2] YLDDiv: Az aktuális osztalékhozam alakulása adja az alapját az előrejelzésnek (itt beszéltünk erről).
[6] GORDiv,E = YLDDiv + gE: Osztalékhozam és a jövőbeni nyereségnövekedés.
[7] GORDiv,Div = YLDDiv + gDiv: Osztalékhozam és a jövőbeni osztaléknövekedés.
[11] ΔVTRCAPE: Shiller-féle CAPE mutatón alapuló jelzés (lásd itt).
[13] ΔVBUF: A Buffett-indikátor néven ismert összefüggés (lásd itt).
[15] ΔVEW: Négy értékeltséget mérő összefüggés (Shiller és Buffett indikátor is benne van) átlaga adja az előrejelzést, kombinált módszer.
Melyek a legjobb modellek?
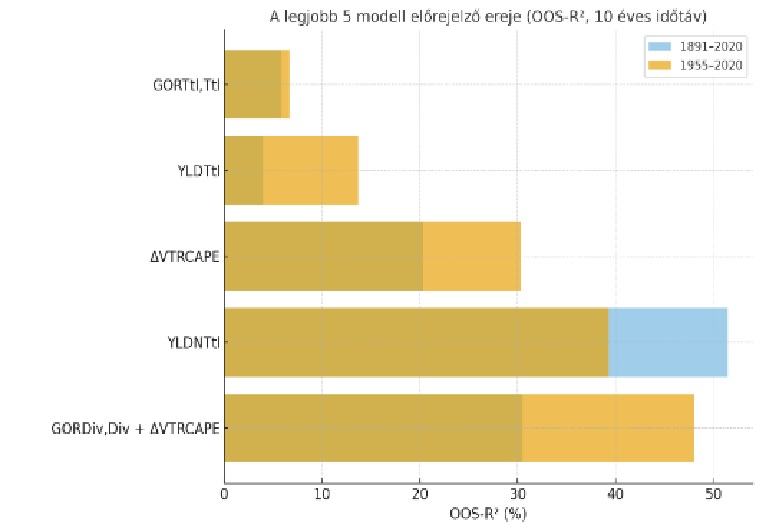
A kutatás szerint öt olyan modell van, amely a több mint 130 éves adatsoron is kimutatható előrejelző erővel bír. Ezek különböző elven próbálják megragadni, mikor olcsó vagy drága a piac, és milyen jövőbeli hozamokra számíthatnak a befektetők. Ahogy az alábbi ábrán látható, a legjobban teljesítő modell, a GORDiv,Div + ΔVTRCAPE, a klasszikus Gordon-féle képletet bővíti ki. Ez egyszerre veszi figyelembe az aktuális osztalékhozamot, az osztalékok növekedési ütemét és a piaci értékeltséget. Eszerint, ha a piac olcsó, a cégek gyorsan növelik osztalékaikat, és a befektetők magas hozamot követelnek, a modell magas jövőbeli hozamot vetít előre. A második legerősebb mutató, a YLDNTtl, a vállalatok által ténylegesen a részvényesekhez visszajuttatott pénzáramot méri. Nemcsak az osztalékokat, hanem a részvény-visszavásárlásokat is figyelembe veszi, vagyis azt mutatja meg, mekkora „kézzelfogható hozamot” kap a befektető. Ha a cégek sok pénzt osztanak vissza, az jellemzően magasabb jövőbeni hozamokkal jár. A harmadik helyen a ΔVTRCAPE áll, amely a Shiller CAPE továbbfejlesztett, total return alapú változata. Ez a mutató az értékeltségre koncentrál: mennyire olcsó vagy drága a piac a hosszú távú profitokhoz képest. Minél alacsonyabb a TRCAPE, annál nagyobb a várható hozam.
Az ábrán látható OOS-R² értékek azt mutatják meg, hogy az egyes modellek mennyivel pontosabban jelezték előre a jövőbeli részvénypiaci hozamokat, mint egy egyszerű, múltbeli átlaghozamra épülő becslés. Ez az úgynevezett out-of-sample (mintán kívüli) tesztelés azt méri, mennyivel csökken a modell előrejelzési hibája az alapforgatókönyvhöz képest. A legjobb modellek esetében az értékek 30–50% közé esnek, ami azt jelenti, hogy ezek a módszerek a jövőbeli hozamok becslési hibáját közel a felére csökkentették. Fontos azonban látni, hogy ez nem a teljes variancia megmagyarázását jelenti, hanem az előrejelzési hiba csökkenését – vagyis a modellek nem látnak a jövőbe, de statisztikailag kimutathatóan jobb becslést adnak, mint a múltbeli átlag.
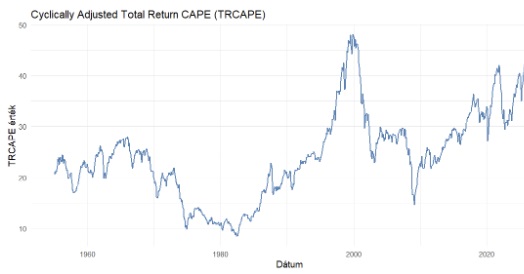
A legegyszerűbben követhető mutató a fentiek közül a TRCAPE. Ez a modell a háromkomponensű megközelítésen alapul, azaz egyszerre veszi figyelembe az aktuális osztalékhozamot, a nyereség vagy osztalék növekedési ütemét, valamint az értékeltség-változást. Ez gyakorlatilag a Shiller féle CAPE mutató továbbfejlesztett, osztalék-visszaforgatással korrigált változata. Technikailag a TRCAPE egy olyan CAPE mutató, amely nem a tőzsdeindex árindexét, hanem a tőzsdeindex total return (osztalékot is tartalmazó) indexét használja. Amikor a TRCAPE alacsony, az a múltbeli átlaghoz képest olcsóbb részvénypiacot jelez, ami jellemzően magasabb jövőbeni hozamokat vetít előre. Ezzel szemben, amikor a TRCAPE magas, az túlértékelt állapotra utal, és alacsonyabb jövőbeli hozamot jelent. A mutatóra épülő portfólióallokáció sharpe rátája (a hozam–kockázat arány) 60–80 százalékkal magasabb lett, mint a múltbeli átlaghozamok kivetítésével számított portfóliók sharpe rátája. Vagyis a befektetők, akik az ilyen típusú modellből származó jelzéseket követik (például akkor növelik részvénysúlyukat, amikor a TRCAPE alacsony) magasabb kockázatmentesített hozamot érhetnek el.
A tanulmány szerint a részvénypiac hosszú távú hozamainak előrejelezhetősége időtávfüggő jelenség. Míg 10–20 éves horizonton a különböző modellek – például a CAPE vagy a total return alapú TRCAPE – még képesek kimutathatóan jobb előrejelzést adni, addig 30 éves időtávon már eltűnik ez az előny. Ennek oka, hogy három évtized alatt a piacok hajlamosak visszatérni a hosszú távú egyensúlyi szinthez, vagyis a túlárazások és alulárazások kiegyenlítődnek. Egy másik fontos tényező, hogy ilyen hosszú idő alatt több gazdasági és monetáris rezsimváltás is bekövetkezik. Az infláció, a kamatszint, sőt a befektetői kockázatvállalási hajlandóság is lényegesen megváltozhat, ami eltünteti az értékeltségi mutatók hatását. Ez az adaton is kimutatható, hiszen 30 éves időtávon az előrejelző erő (R²) gyakorlatilag nullára csökken, vagyis a modellek már nem teljesítenek jobban, mint ha egyszerűen a múltbeli átlaghozamot vetítenénk a jövőre. Azt látjuk tehát, hogy rövid és középtávon a piac értékeltsége számít, hosszú távon azonban minden visszatér az átlaghoz, és a történelem végül kiegyenlíti a befektetői kilengéseket.
A 26 módszer pontossága 10 éves időtávon
A kutatásban a szerzők egy dinamikus eszközallokációs modellt alkalmaztak, amelyben a részvények és kötvények aránya nem állandó, hanem évről évre a várható részvénypiaci kockázati prémium alakulásához igazodik. Ez gyakorlatilag azt jelenti, hogy a befektető akkor vállal több részvénykitettséget, amikor a modellek magas jövőbeli részvénypiaci hozamot jeleznek a kötvényhozamokhoz képest, és akkor csökkenti a részvényarányt, amikor a várható prémium alacsony. A kockázati prémium a részvénypiac és a kockázatmentes (általában 10 éves államkötvény) hozam különbsége:
- Ha például a modellek szerint a részvénypiac következő 10 évben évi 7%-os reálhozamot,
- míg a kötvénypiac évi 2%-os hozamot kínál, akkor a kockázati prémium 5%.
- Ez magas értéknek számít, így a modell növeli a részvények súlyát a portfólióban.
Ezzel szemben, ha a várható részvényhozam 3%, a kötvényhozam pedig 2,5%, a prémium mindössze 0,5%, tehát alacsony, és a modell ilyenkor csökkenti a részvénykitettséget, például 40%-ra, a maradékot kötvényekben vagy készpénzben tartva. Ez a módszer tehát nem piaci időzítést jelent, hanem kockázatarányos súlyozást:
- amikor a részvények várható kompenzációja nagy, a befektető több kockázatot vállal;
- amikor a prémium csekély, visszavesz a részvénysúlyból, mert a pluszkockázatért cserébe már nem kap elég hozamot.
Konkrét példaképpen képzeld el azt az esetet, hogy a TRCAPE értéke 40, akkor ennek reciproka (1/40=2,5%) adja a kockázati prémium várható jövőbeli értékét. Tegyük fel, hogy a 10 éves lejáratú amerikai államkötvény hozama 4%, így a részvénypiac többlethozama negatív, azaz a modell alulsúlyozza a részvényeket, és felülsúlyozza a kötvényeket.
A kutatók az így kialakított portfóliókat visszatesztelték az 1891–2020 közötti időszakra, és azt találták, hogy ez a „prémiumhoz igazított” súlyozás átlagosan:
- 60–80 százalékkal magasabb Sharpe-rátát eredményezett,
- a portfólió maximális vesztesége (Value-at-Risk) pedig közel felére csökkent,
- a hagyományos, fix (például 60% részvény – 40% kötvény) stratégiához képest.
A következő táblázatban több időszakra lebontva (1891-2020, 1955-2020, 1988-2020) láthatjuk az egyes hozam-előrejelző módszerek hatékonyságát. A sharpe ráta sor a módszerrel elérhető egységnyi kockázatra vetített hozamot mutatja (magyarázat itt). Érdemes összevetni a történelmi átlagon alapuló (Historical Mean) előrejelzés sharpe rátáival (0,19, 0,26, 0.31).
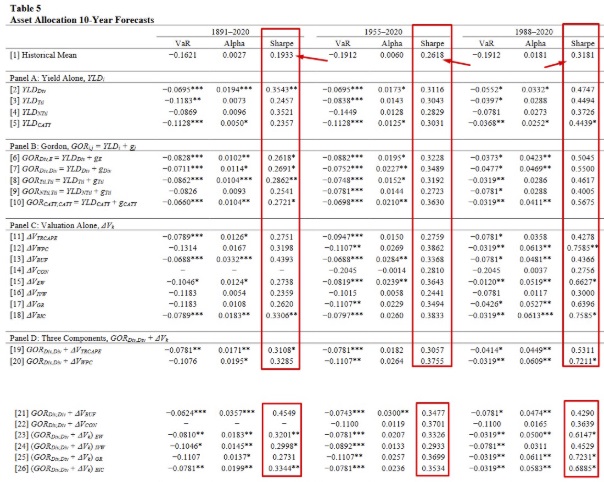
A táblázatból körvonalazódik, hogy az összetettebb modellek lényegesen magasabb sharpe-rátát eredményeztek 10 éves időtávon, mint a történelmi átlag kivetítése. Ennek részben az az oka, hogy 10 éves időtávon nagy az ingadozás a részvénypiac kockázati prémiumában, így a múltbeli hozamokból kiinduló passzív befektetők nagyobb kockázatot vállalnak.
A 26 módszer pontossága 20 éves időtávon
Ahogy azonban az alábbi táblázatból kiderül, 20 éves távon már sokkal stabilabb a részvénypiac kockázati prémiuma, így a passzív befektetéssel elérhető hozamot jelentősen nem tudják felülmúlni a különböző előrejelző-módszerek.
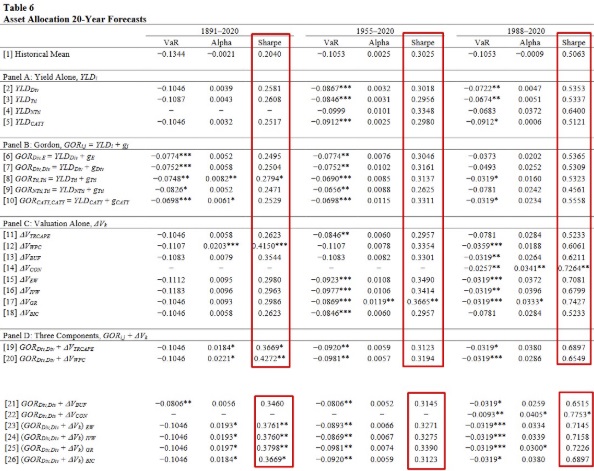
Összességében az látható a fentiekből, hogy számos olyan módszer létezik, melyekkel rövidebb időtávon (10-20 év) jobb eredményt lehetett elérni, mint a történelmi átlag jövőbe történő kivetítése. A javuló sharpe-ráták azt mutatják, hogy a felsorolt összefüggéseket, illetve ezek egy részét célszerű a portfólió-kialakítás során figyelembe venni. Ez nem feltétlenül jelenti azt, hogy nem tartunk részvényt a portfólióban bizonyos időszakokban. Sokkal inkább arra használhatók a módszerek, hogy súlyozzuk a részvény-kötvény arányát a portfólión belül, így például, ha a jövőbeni kockázati prémium várhatóan alacsony, akkor alacsonyabb arányban tartunk részvényeket. Fontos azt is látni, hogy az időtáv növekedésével egyre kisebb jelentősége van a módszereknek, és egyre kisebb az eltérés a történelmi átlag jövőbeni kivetítéséhez képest.
Portfólióallokáció a TRCAPE alapján
Az alábbi kalkulátor segíthet megérteni a részvény-kötvény arány változásának mechanizmusát. A kalkulátor kizárólag oktatási célokat szolgál. Az eszköz az alapvető pénzügyi összefüggések – például a várt részvénypiaci prémium és a kockázatkerülés hatásainak – megértését segíti. Az eredmények nem alkalmasak tényleges portfólióarányok meghatározására vagy jövőbeli piaci hozamok előrejelzésére.
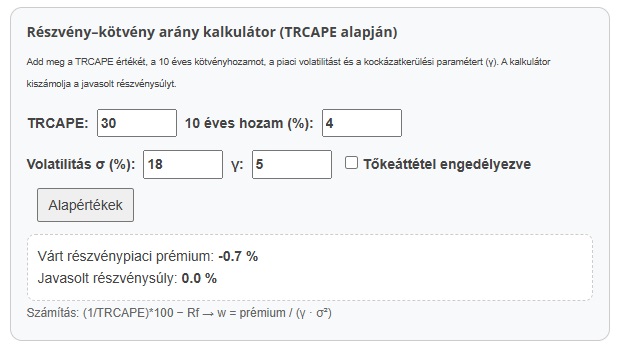
A kalkulátorban a gamma (γ) a relatív kockázatkerülési együttható:
- Kis γ (pl. 2–3) → kockázatkedvelőbb, több részvényt tart a portfólióban.
- Nagy γ (pl. 6–10) → kockázatkerülőbb, kisebb részvényarányt választ.
Matematikailag a klasszikus Merton–Markowitz modell szerint került a kalkulátorba, azaz ha két befektető ugyanazt a prémiumot és volatilitást látja, de egyikük kockázatkedvelőbb (γ = 3), a másik kockázatkerülő (γ = 6),
akkor a γ = 6-os befektető fele akkora részvénykitettséget választ, mert kétszer annyira tart a kockázattól. A gamma becslésére gyakran használják tanácsadók a Dohmen-féle kockázati preferencia kérdőívet, néhány irányadó érték:
- Nagyon kockázatvállaló 0,5-2 γ
- Átlagos, kiegyensúlyozott 3-5 γ
- Konzervatív, kockázatkerülő 6-10 γ
- Nyugdíj előtt álló 10-15 γ
A grafikon Shiller professzor adatai alapján számított TRCAPE mutató alakulását mutatja be, amely 1950 óta 8 és 45 pont közötti tartományban ingadozott.